Boolean Satisfiability problems (SAT) consists of finding a valid assignment (model) for a set of Boolean variables. It was the first problem proven to be NP-Complete which allowed reducing many NP-Complete problems to it. Because of this, it is one of the pillars of Computer Science.

An extension to SAT is Pseud-Boolean optimization problems. Unlike SAT, which can only express binary relationships among variables, Pseudo-Boolean optimization can formalize more complex relationships. These problems are defined in the following manner:

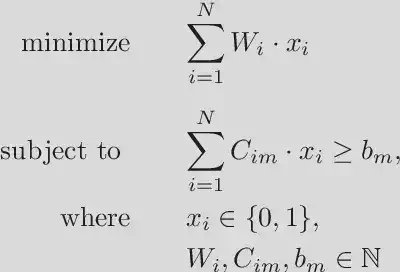
Example: Knapsack problem

Given a set of items, each one with a value and a weight, and a knapsack with a maximum capacity, the goal is to select some objects to put inside the knapsack in a way that the weight is not bigger than the knapsack’s capacity and the total value is maximised.

The variables for this problem, given $n$ objects, are: $$o_1, o_2, \ldots , o_n \text{for the objects}$$ $$w_1, w_2, \ldots , w_n \text{for the weights}$$ $$v_1, v_2, \ldots , v_n \text{for the values}$$ There is only one constraint which represent the maximum capacity of the knapsack problem: $$w_0 o_0 + w_1 o_1+ \ldots w_n o_n \leq knapsack’s \ capacity$$ And the cost function: $$v_0 o_0 + v_1 o_1+ \ldots v_n o_n $$

SAT Solvers

A SAT solver is a tool that aims at solving Boolean Satisfiability problems. However, they take as input Boolean formulas in Conjunctive Normal Form (CNF). In this project, we propose an efficient encoding for converting Pseudo-Boolean minimisation problems into CNF constraints. If this encoding is not efficient, the size and difficulty of the problem can increase exponentially.

Proposed encoding

The proposed encoding is based on the idea that if a function’s primes cover a small space then a lot of clauses will be required when encoding it into a CNF. For more details see the slides.

Notes

1. https://www.semanticscholar.org/paper/MPBO-A-Distributed-Pseudo-Boolean-Optimization-Santos-Godinho/52ee5d8996c6f6d5caa43ad35155f404ddc584e3

2. https://en.wikipedia.org/wiki/Knapsack_problem

This dissertation focuses on creating a robust environment to solve Pseudo-Boolean Optimization (PB) problems, a specific type of optimization commonly used in fields like Artificial Intelligence, Planners, Computer Vision, and Circuit Design. The main goal is to reduce the time required to solve these problems by using an efficient C++ library for representing and optimizing PB problems.

Key Contributions

The project builds on previous work by developing a C++ library for PB minimization, using the PBLib to translate Pseudo-Boolean constraints into Conjunctive Normal Form (CNF) for solving with SAT solvers. The following methods and features were implemented:

1. Pseudo-Boolean Formula Representation: A library that allows smooth representation and manipulation of PB formulas.
2. Optimization Algorithms:
   • Linear Search: Sequentially checks potential solutions to find the minimum.
   • Binary Search: More efficient search for minimum values by dividing the search space.
3. Timeout Strategies:
   • General Timeout: Limits the total execution time, returning the best solution found.
   • Simple Timeout: Stops individual solver calls after a set time to ensure timely results.

Results and Evaluation

The library was evaluated using benchmarks to compare the efficiency of the linear and binary search methods. The timeout strategies were particularly beneficial in cases where obtaining a timely solution was more critical than achieving optimal results.

Conclusion

This project successfully reduced the time required to solve Pseudo-Boolean minimization problems, making it more accessible to fields like AI and Planners. The developed tools provide an easier interface to work with PB minimization problems, especially for C++ programmers. Future work could focus on improving multi-threading support and further optimizing search algorithms.

Source Code: GitHub Link